Um pouco de Cálculo

Um sistema dinâmico é uma regra que associa estados passados a estados futuros. Lembra-se daqueles desafios lógicos em que você tem uma sequência de números e tem que descobrir a regra que os gera, para descobrir o próximo? Algo como 1, 1, 2, 3, 5 e você deve adivinhar que o próximo é 8. 

Neste caso, temos a regra xn+1=xn+xn−1, chamada regra de Fibonacci. Uma regra associando estados passados (o xn e o xn−1, que são o estado anterior e o antes do anterior) a estados futuros (xn+1), pois podemos continuar para obter todos os seguintes. 

Claro que não estamos restritos a isso, podemos definir muitas regras e até estabelecer regras em espaços que não são discretos e bonitinhos como o do exemplo.

Com isso, dá para perceber que muita coisa é um sistema dinâmico. A grande exigência é que a regra deve ser determinística, ou seja, começando em um ponto o sistema deve caminhar em uma direção específica. Se voltar ao ponto de partida, o sistema deve percorrer percorrer o mesmo caminho, ou efetuar uma órbita, como gostamos de chamar.

Um exemplo interessante dos dois primeiros em sistemas dinâmicos é a equação logística, algo de definição bem simples e resultados complicados. Assim como nós antes tínhamos uma sequência definida com a regra de Fibonacci, vamos pensar em outra regra: xn+1=r.xn(1−xn), onde r é um número entre 1 e 4. Parece simples, e nem parece muito diferente da outra, mas dependendo do valor de r você vai descobrir que essa a sequência gerada sai do controle rapidamente.

Vejamos o que acontece quando começamos no valor x0=0,1 e com r=1,2. Primeiro calculamos o próximo passo: x1=r.x0(1−x0) =1,2.0,1(1−0,1)=0,108. Para calcular o próximo passo, continuamos com a regra: x2=r.x1(1−x1) =1,2.0,108(1−0,108)=0,1156032. Não vou escrever linha por linha, mas um gráfico revela o futuro dessa conta, ela converge para um valor específico.

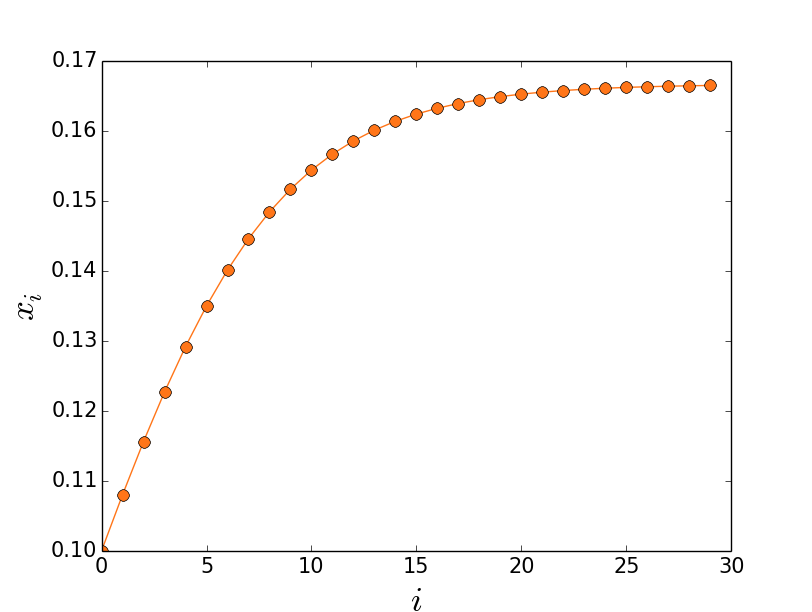
Com esse gráfico você pode achar que esse sistema é tranquilo, que outros valores vão também convergir, que tudo caminha para um valor bonito e estável. Nada podia estar mais longe da verdade. Veja o que acontece quando trocamos r por 3,1.

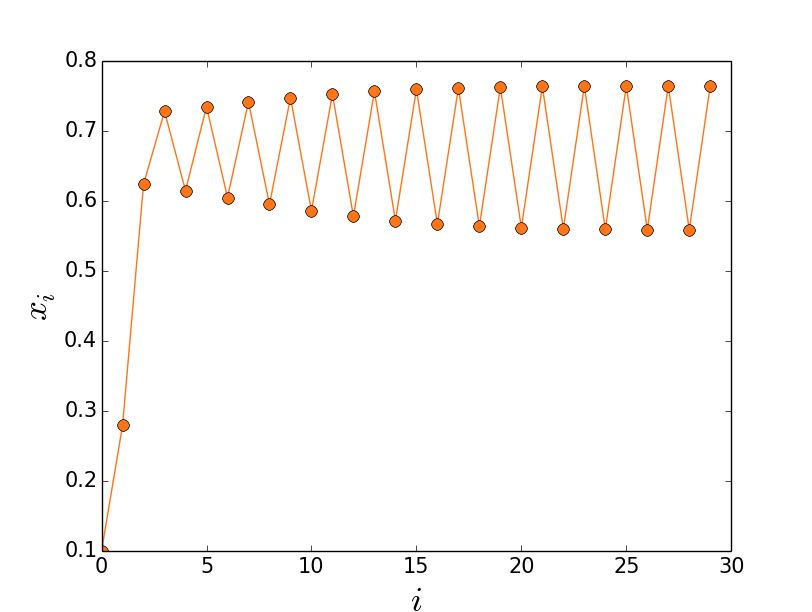
Com esse valor de r, o sistema não converge para um valor, mas para dois valores. Esse comportamento não é lá muito normal, mas piora, veja o que acontece quando colocamos r=3,5.

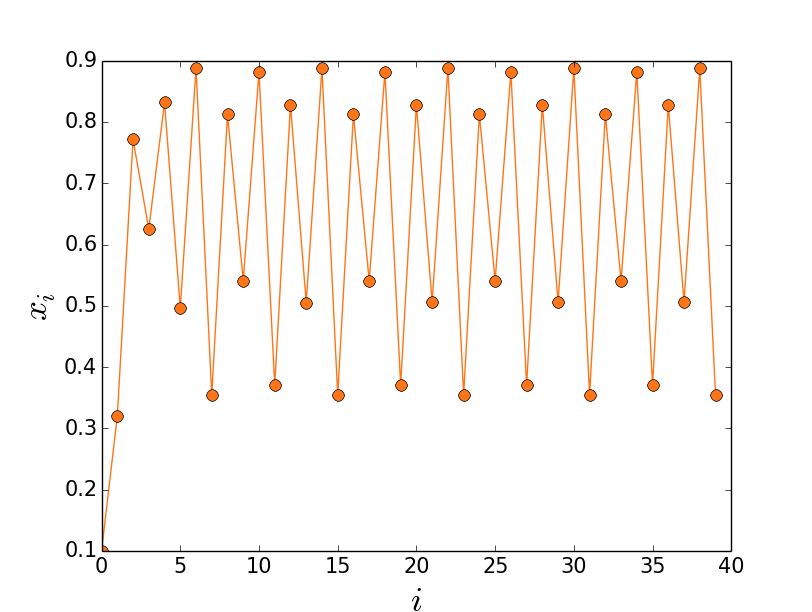
Nesse caso, o sistema converge para quatro valores. Conforme aumentamos o valor de r, o sistema fica cada vez mais instável e converge para cada vez mais valores diferentes. Chega um ponto que podemos nos perguntar: converge mesmo? Não seriam tantos valores que a própria noção de convergência já perde o sentido?

Esse sistema dinâmico converge para um valor apenas quando r está entre 1 e 3. Para um r entre 3 e 3,45, ele converge para dois. Quando r está entre 3,45 e 3,544, o valor de xn pipoca entre quatro possibilidades e entre 3.54 e 3.56 teremos oito possibilidades. 

Não apenas esses valores aumentam exponencialmente, o intervalo de r em que eles acontecem fica cada vez menor. Refletido a respeito, o primeiro intervalo é quase cinco vezes maior que o segundo, enquanto o segundo também é quase cinco vezes maior que o terceiro. Essa relação entre os intervalos, se fizermos uma sequência com ela, converge para um valor, chamado constante de Feigenbaum. 

Quando chegamos a r=3,7, na verdade bem antes disso, torna-se completamente impossível prever os valores desses sistema. O único jeito de obter o valor na centésima iteração é calcular todas as noventa e nove anteriores. Veja como fica nosso gráfico para r=3,7.

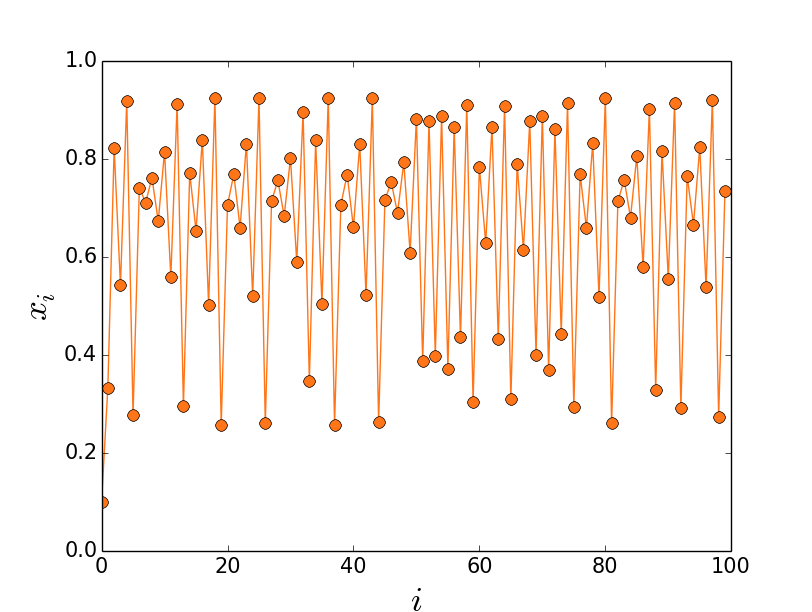
E talvez nisso surja uma das perguntas mais interessantes de caos, fractalidade e sistemas dinâmicos: como pode uma regra tão simples gerar um resultado tão complicado e imprevisível? Como pode tanta complexidade emergir de uma única lei? O caráter matemático dessas perguntas é profundo, e as implicações são maiores do que imaginamos olhando pela primeira vez.