Atratores Estranhos

Em 1963, quando Edward Lorenz (1917-2008), se interessou pelo problema de convecção na atmosfera terrestre, simplificou drasticamente as equações de Navier-Stokes da mecânica dos fluidos, famosas por suas inextrincável complexidade. O modelo atmosférico de Lorenz é o que os físicos chamam de modelo de brinquedo (modelo simplificado) : mesmo que não haja grande coisa a ver com a realidade, Lorenz não demorou a concluir que se tratava de um modelo matemático muito interessante.

 As equações de Lorenz envolvem apenas três números x, y e z, de modo que cada ponto (x, y, z) do espaço simboliza um estado da atmosfera e a evolução consiste em seguir um campo de vetores.

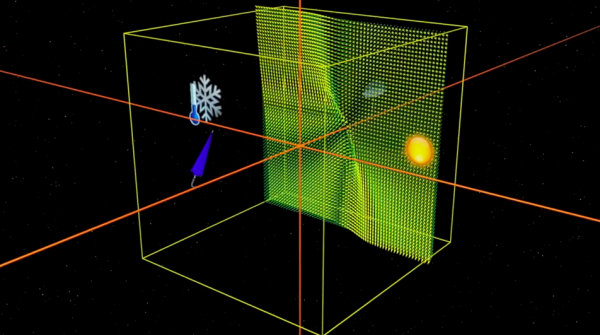
Compreender a evolução que o tempo provoca na atmosfera virtual de Lorenz consiste em seguir uma trajetória deste campo de vetores. Não nos esqueçamos que se trata de um modelo de brinquedo e que o objetivo é tentar compreender as grandes linhas de um comportamento complexo. 

Se consideramos duas atmosferas quase idênticas, portanto representadas pelos centros de duas bolinhas extremamente próximas, rapidamente as duas evoluções se separam de maneira significativa: as duas atmosferas tornam-se completamente diferentes. Lorenz pôde constatar, no seu modelo, a dependência sensível das condições iniciais, o caos.

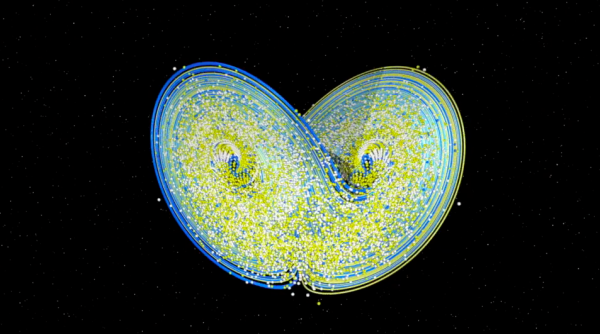
Mas o mais interessante, partindo de  um grande número de ambientes virtuais,  embora meio loucos e pouco previsíveis, as trajetórias parecem acumular-se num mesmo objeto em forma de uma  borboleta, popularizada com o nome de atrator de Lorenz, um atrator bastante estranho... 

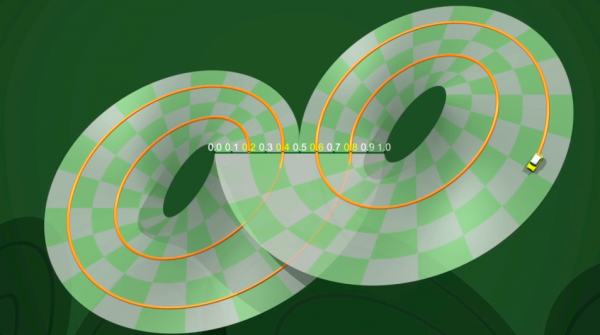
Compreender o atrator de Lorenz é um desafio verdadeiramente científico. Com o que se parece precisamente? Como se comporta sua dinâmica interna? Foi por tentar responder a estas questões que, no ano de 1970, Birman, Guckenheimer e Williams propuseram um modelo simples que se pode construir com tiras  de papel: como na ferradura, passa - se de uma dinâmica em tempo contínuo para uma dinâmica em tempo discreto.

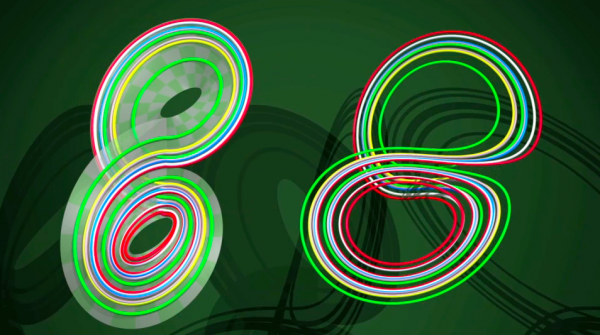
Foi necessário esperar até 2001 para que o matemático Warwick Tucker demonstrasse que as tiras de papel descrevem bem o movimento de Lorenz: para cada trajetória no atrator de Lorenz, existe uma trajetória nas tiras de papel que se comporta exatamente da mesma forma. Mesmo que tudo isto seja ainda muito simples em relação ao verdadeiro fenômeno meteorológico,   é uma ilustração do fato que os matemáticos adoram as coisas simples.

Previsão do tempo 

A complexidade do modelo era um aspecto crítico dos experimentos, porque os computadores da época eram lentos: Lorenz dispunha de um Royal McBee LGP-30 com 16k de memória interna, capaz de realizar 60 multiplicações por segundo. Para um sistema de doze equações diferenciais, cada passo da integração numérica tomava 1 segundo. Após diversas tentativas, Lorenz acabou adotand um modelo com 3 equações introduzido por B. Saltzmann, que veio a ser chamado sistema de Lorenz.

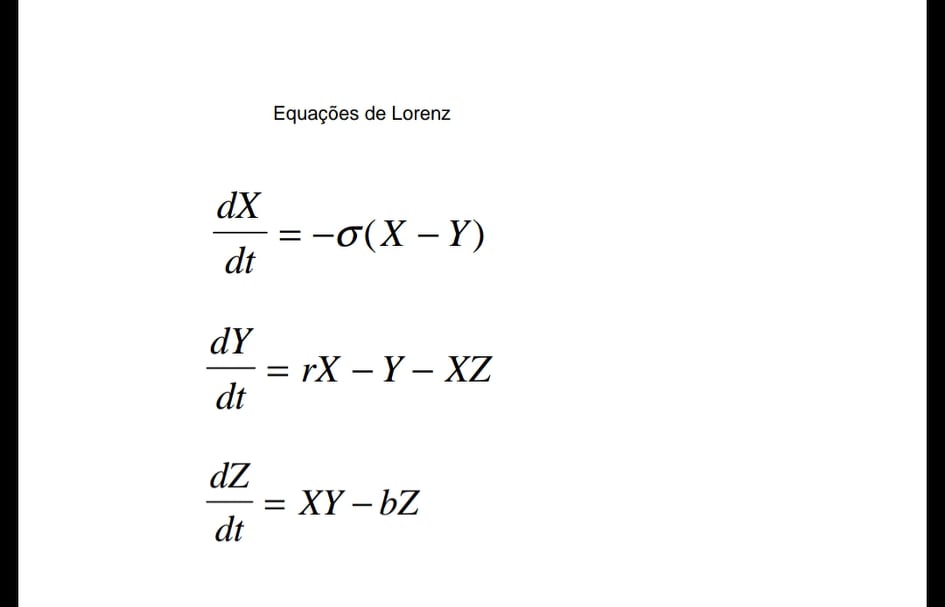
X é proporcional à intensidade da convecção. X=0 implica que não há movimento convectivo, ou seja, o calor é transportado apenas por condução. 

X>0 implica circulação horária e X<0 circulação anti-horária. 

Y é proporcional à diferença de temperatura entre as correntes de fluido ascendente e descendente. 

Z é proporcional à distorção do perfil de temperatura vertical, relativamente a um perfil linear. 

Para Z=0, a temperatura decresce linearmente. 

Sensitividade Para acelerar os cálculos, Lorenz imprimia os resultados com apenas 3 dígitos decimais, embora os cálculos fossem realizados com 6 dígitos. Em algum momento reintroduziu um resultado como novo dado inicial:

o.707107

0.121320      0.121

0.363961      0.363

0.091883      0.089   

0.275649      0.267

0.826948      0.801

0.480843      0.403 

0.442530      0.209

Para sua surpresa, o novo cálculo divergia do anterior: as previsões para 4 dias mais tarde eram totalmente distintas. Inicialmente, Lorenz acreditou que isso se devia a falha mecânica. As consequências desta descoberta de que o modelo é sensitivo aos dados iniciais foram profundas. 

Atratores estranhos

 Um atrator é uma região do espaço de configurações que fica invariante quando o tempo passa e que atrai muitas (ou até todas as) configurações próximas. Ruelle e Takens não definiram "estranho", nem conheciam bons exemplos. De fato, o sistema de Lorenz era um exemplo espetacular dessa noção. E atrator estranho acabou significando um atrator tal que as trajetórias que convergem para ele dependem sensitivamente do ponto inicial. Mas o trabalho de Lorenz ainda era mal conhecido, e Ruelle e Takens só tinham como exemplos os atratores hiperbólicos de Smale.

Sistema de Lorenz:

• Primeiro Atrator caótico
• Sensibilidade ás condições iniciais em um fluido (modelo meteorológico simplificado)

Variáveis: x, y, z →  espaço de fase tridimensional parâmetros de controle: σ, r, b.

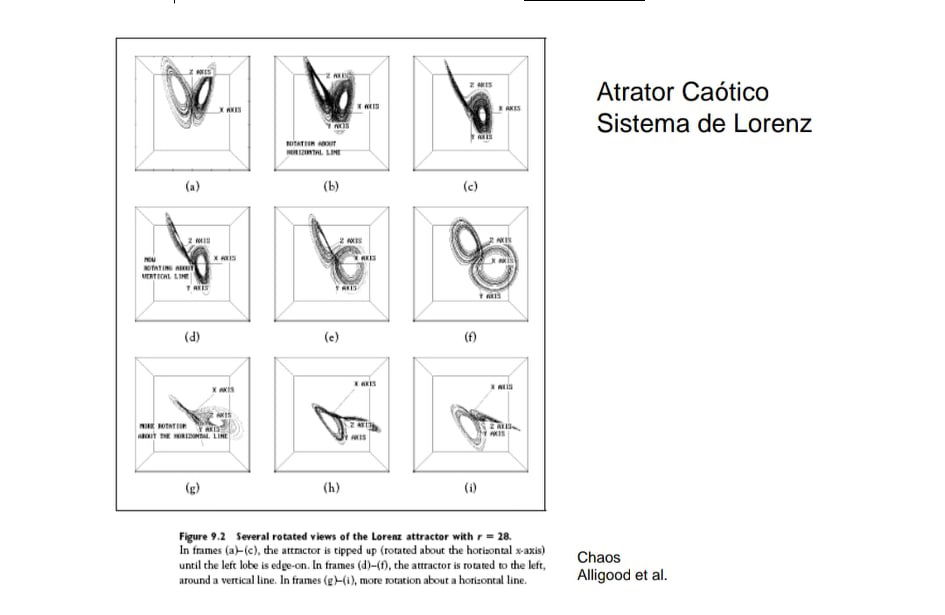
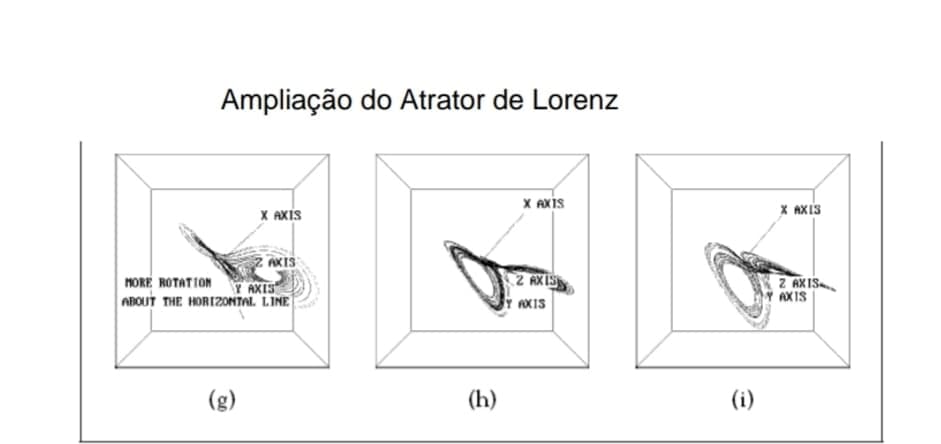Cada ponto traçado no mapa em forma de tenda é um par (zn, zn+1) de coordenadas z máximas de loops da trajetória, uma seguindo a outra. A natureza quase quase unidimensional do mapa surge da contração de volume muito forte.

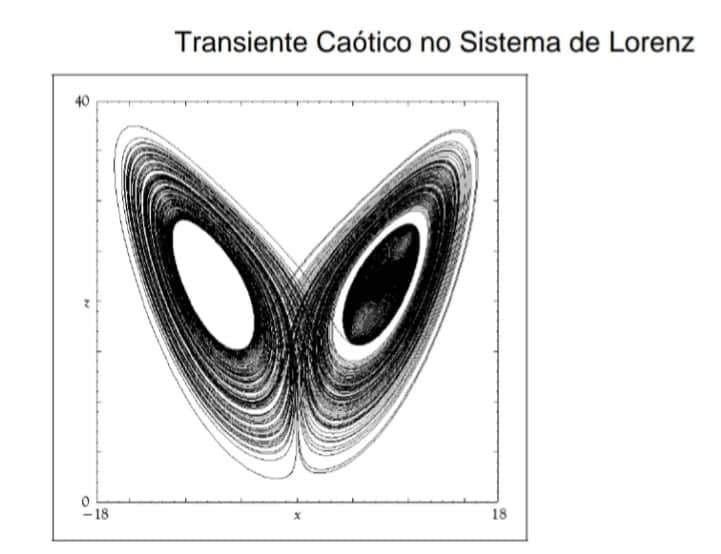Uma trajetória do sistema Lorenz foi plotada usando b=8/3 e σ= 10, os mesmos valores que Lorenz usou, mas aqui r=23. Quando r1≅ 24.06 há sim.  

Variáveis: x, y, z espaço de fase tridimensional Parâmetros de controle : a , b, c.