Mude uma coisa, mude tudo

Teoria do Caos é, na realidade, um conjunto de teorias que determinam uma teoria que visa compreender os Sistemas Dinâmicos Não Lineares. Estes, por sua vez, seriam pesquisas voltadas à compreensão dos meios aleatórios e imprevisíveis dos sistemas, tanto complexos, como também dinâmicos 

Um termo mais acurado, o caos determinístico, sugere um paradoxo porque liga duas noções que são familiares e comumente consideradas incompatíveis. O primeiro é o da aleatoriedade ou imprevisibilidade, como na trajetória de uma molécula em um gás ou na escolha do voto de um indivíduo em particular de fora de uma população. Nas análises convencionais, a aleatoriedade foi considerada mais aparente do que real, decorrente da ignorância das muitas causas no trabalho. Em outras palavras, acreditava-se comumente que o mundo é imprevisível porque geralmente se acredita que o mundo é imprevisível porque é complicado. A segunda noção é a do movimento determinístico, como a de um pêndulo ou planeta, que foi aceita desde a época de Isaac Newton como exemplificando o sucesso da ciência em tornar previsível aquilo que é inicialmente complexo.

Nas últimas décadas, no entanto, estudou-se uma diversidade de sistemas que se comportam de forma imprevisível, apesar de sua aparente simplicidade e do fato de que as forças envolvidas são governadas por leis físicas bem compreendidas. O elemento comum nesses sistemas é um alto grau de sensibilidade às condições iniciais e à maneira como elas são colocadas em movimento.

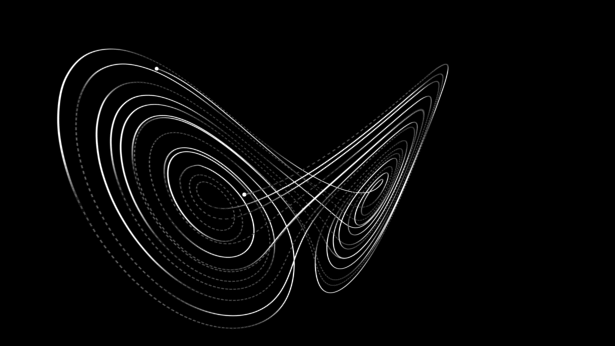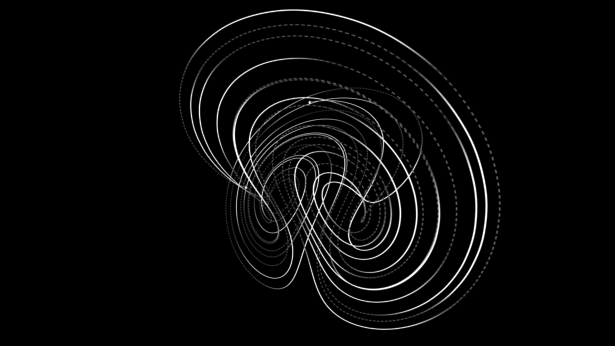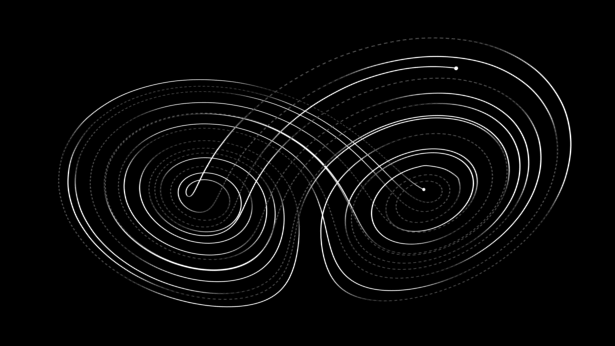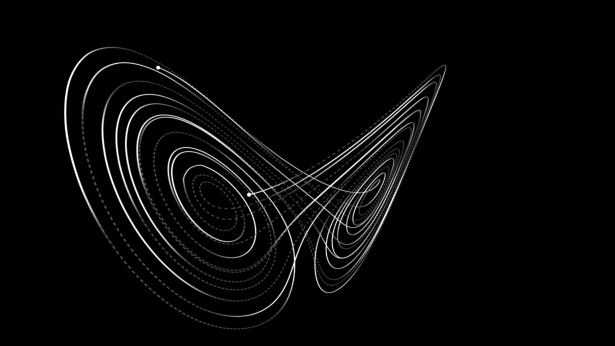
 Por exemplo, o meteorologista Edward Lorenz descobriu que um modelo simples de convecção de calor possui imprevisibilidade intrínseca, uma circunstância que ele chamou de “efeito borboleta”, sugerindo que o mero bater de asas de uma borboleta pode mudar o clima. Um exemplo mais simples é a máquina de pinball: os movimentos da bola são precisamente governados por leis de rolamento gravitacional e colisões elásticas - ambas totalmente compreendidas -, mas o resultado final é imprevisível.

 Na mecânica clássica, o comportamento de um sistema dinâmico pode ser descrito geometricamente como movimento em um “atrator”. A matemática da mecânica clássica efetivamente reconheceu três tipos de atratores: pontos únicos (caracterizando estados estacionários), loops fechados (ciclos periódicos) e tori (combinações de vários ciclos). Na década de 1960, uma nova classe de "atratores estranhos" foi descoberta pelo matemático americano Stephen Smale. Em atratores estranhos, a dinâmica é caótica. 

Mais tarde, foi reconhecido que os atratores estranhos têm estrutura detalhada em todas as escalas de ampliação; Um resultado direto desse reconhecimento foi o desenvolvimento do conceito de fractal (uma classe de formas geométricas complexas que comumente exibe a propriedade da auto-similaridade), o que levou, por sua vez, a desenvolvimentos notáveis em computação gráfica. Aplicações da matemática do caos são altamente diversificadas, incluindo o estudo do fluxo turbulento de fluidos, irregularidades no batimento cardíaco, dinâmica populacional, reações químicas, física do plasma e movimento de grupos e aglomerados de estrelas.

Características da Teoria do Caos e uso

É necessário partir do princípio que rege a teoria do caos: o acaso. O acaso é um fenômeno oriundo de representações numéricas; equações matemáticas. Estas apresentaram pontuais graus de precisão, e evidenciam acontecimentos caóticos entre si.

As equações, entretanto, se materializam por meio de gráficos tridimensionais no momento em que um evento é tido como caótico.

Por meio disso, nos sistemas considerados não lineares, cuja resposta a um distúrbio não é totalmente proporcional à intensidade provocada, as equações evolverão taxas com variabilidade aguda.

Assim, as mudanças seguirão relação direta de causa e efeito, sobre a denominação do que se entende por Efeito Borboleta. Dessa forma, os resultados obtidos dessa relação são influenciados de acordo com fatores numéricos instáveis e totalmente aleatórios.

São resultantes sensíveis e divergentes às condições iniciais, que determinarão o resultado futuro. Assim, de forma básica, uma mudança ínfima em quaisquer das condições pode resultar em ligações com eventos futuros que provoquem intensas alterações.

Proporcionalmente, quando um movimento se torna previsível, o gráfico na teoria do caos é espiralado, e quando os cálculos apresentam gráficos com representações caóticas, e não-harmônicas, são chamados de fractais.

A origem dos fractais é complexa e abstrata, evidenciando um formato geométrico atípico. Dessa maneira, a metodologia abordada pela Teoria do Caos é utilizada para compreender:

• Variações em investimentos imprevisíveis (bolsas de valores e oscilações);
• Avaliação de fenômenos meteorológicos;
• Desenvolvimento e crescimento populacional;
• 
  

Além de outros casos, a Teoria do Caos procura a avaliação do contexto como um todo. A busca é por prever algo que depende de coalizão de eventos, cruzamento de fatos com contexto póstero indefinido.

Pontos Fortes da Teoria do Caos

A Teoria do Caos tem amplas aplicações na ciência moderna e era da tecnologia. Gestão e comunicação poderão ver uma mudança de paradigma, assim como vários outros ramos de negócios.

Pesquisa e estudo neste ramo por acadêmicos pode ser extramente útil para o mundo dos negócios e das finanças.

Pontos Fracos da Teoria do Caos

As restrições na aplicação da Teoria do Caos se dão principalmente pela escolha dos critérios de entrada. A metodologia usada para computar esses critérios depende das dinâmicas subjacentes aos dados e ao tipo de análise pretendida, que na maioria dos casos é bastante complexa e nem sem sempre precisa.

Não é simples achar uma aplicação direta e imediata da Teoria do Caos no ambiente de negócios, mas mapear o ambiente de negócios com o entendimento do caos é certamente algo cuja aplicação vale a pena ser considerada.