O que é o Efeito Borboleta

O Efeito Borboleta é o conceito que explica a dependência sensível das condições iniciais na Teoria do Caos.
Em outras palavras, diz respeito às pequenas mudanças ou erros que ocorrem no início de qualquer processo e alteram drasticamente os resultados finais, produzindo efeitos desproporcionais.

''Uma coisa tão Simples, quanto o bater de asas de uma borboleta, pode causar um tufão do outro lado do mundo.''  É apenas uma metáfora que representa o fenômeno, pois simboliza a importância de um evento muito simples na produção de consequências de longo prazo e alcance.

O mais incrível sobre o Efeito Borboleta é que ele se aplica a qualquer área das ciências, seja na matemática, física, biologia ou psicologia. Isso porque o conceito pode ser observado em qualquer sistema natural, ou seja, que tenha algum nível de complexidade e dinamismo.

Vamos tomar, como exemplo, usar uma simples espuma de banho na Europa, pode provocar a destruição dos ursos polares lá na Groenlândia!

Isso acontece porque as toxinas liberadas no ambiente percorrem milhares de quilômetros poluindo a água e se acumulando na gordura dos peixes e focas durante anos. Esse animais posteriormente serão comidos pelos ursos.

No final, a concentração de poluentes no sistema dos ursos polares causa desordens de comportamento e falhas na reprodução e no crescimento desses animais.

Viu como uma pequena coisa no início pode ter uma grande consequência no final? Esse é o efeito borboleta, que também tem um nome científico: Dependência sensível das condições iniciais.

O pendulo Duplo  

O problema desse sistema é que nem chorando você consegue prever o movimento dessas bolinhas. O sistema nada tem de aleatório, não há resistência do ar ou atrito, mas a relação entre as duas bolinhas, essa influência mútua causada pelo fio que as liga, torna o problema matematicamente tão complicado que ele toca as raias do impossível: não há homem sobre a terra capaz de escrever a coordenada y de uma bolinha em função da x para qualquer valor de tempo t.

O problema não é a física, você até conhece as equações desse problema. Lembra-se das leis de Newton?, pois bem, você consegue escrever o equivalente às leis de movimento das bolinhas. Essas leis, que são equações, se resolvidas, forneceriam a trajetória exata das bolinhas nesse modelo. O problema é: as equações não podem ser resolvidas exatamente, porque elas são equações muito difíceis.

Isso não nos impede, no entanto, de obter o movimento desse pêndulo estranho, basta explorar nosso amigo computador para isso. As equações são muito difíceis, impossíveis aos mortais no papel e caneta, mas o computador pode, na força bruta, calcular aos poucos cada instante dessa trajetória. Em cada momento, ele consegue estimar com bastante precisão onde o pêndulo estará no instante seguinte. Se esses instantes são bem próximos, a aproximação do computador é boa o suficiente para que o movimento seja descrito. Sentei essa tarde e escrevi um código para simular esse pêndulo, adaptando de outros que vi por aí, o resultado é algo perto disso:

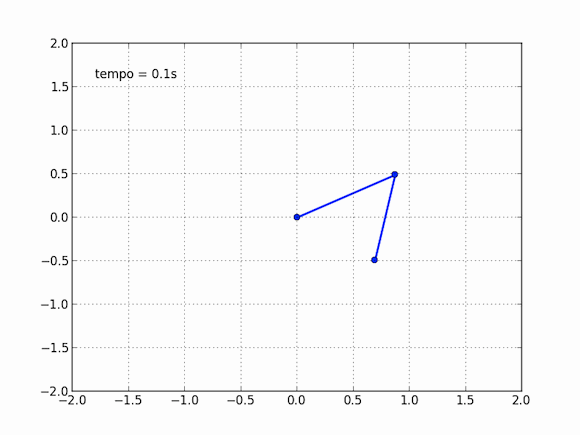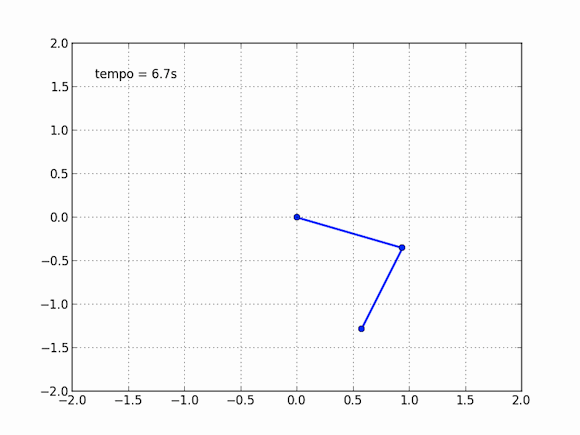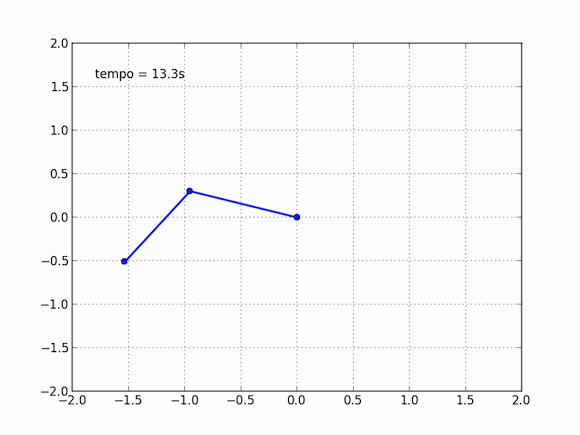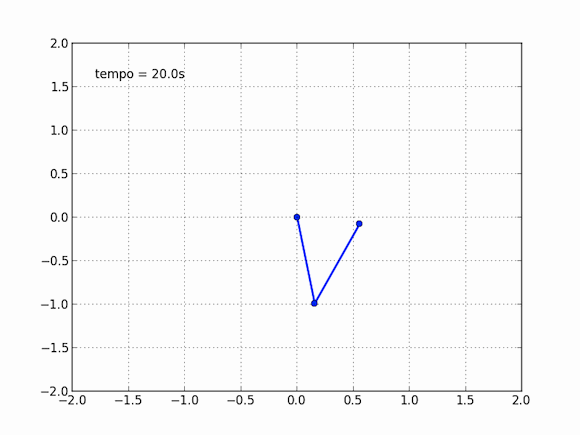
E você também pode dizer que isso não é exato, essa nem é exatamente a resposta do modelo, e isso é verdade, em partes. Essas contas do computador são tão precisas quanto queremos que elas sejam, ora, basta você dizer o quão precisa você quer a conta que ele faz, vai apenas demorar mais ou menos tempo. 

O pêndulo duplo é um caso interessante por diversos motivos. Ele apresenta um fenômeno conhecido como caos, ou, na cultura popular, o efeito borboleta. Sistemas caóticos possuem definição matemática precisa e, como uma de suas características mais marcantes, possuem uma grande dependência de suas condições iniciais. No caso desse pêndulo duplo, dizemos que o lugar onde o pêndulo começa (no exemplo acima, a primeira bolinha forma um ângulo de 120º com a vertical, enquanto a segunda bolinha forma um ângulo de 10º com a vertical) influencia muito mais a trajetória do que você imagina.

Compare com um pêndulo simples, indo de um lado a outro. Sua trajetória são será tão diferente se você lançar o pêndulo de um ângulo de 10° ou se lançar de 9,9999°, você, aliás, terá problemas para dizer se são diferentes. No pêndulo duplo, a história é outra. Para termos uma ideia melhor, a animação foi repetida com dois pêndulos ao mesmo tempo, um azul, como o anterior (120° na primeira e 10° na segunda), e um vermelho, com as configurações levemente alteradas (120° na primeira e 9,9999º na segunda). Veja o que acontece depois de um tempo suficientemente grande: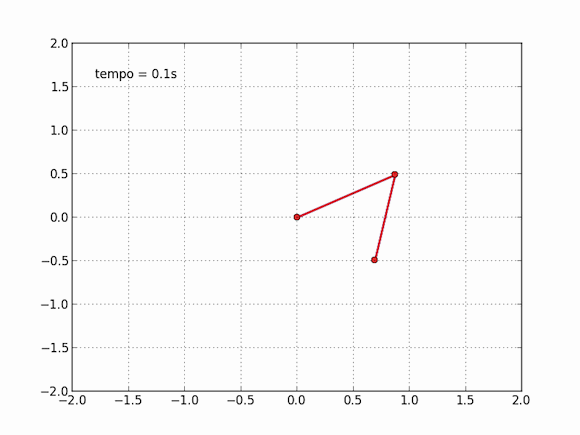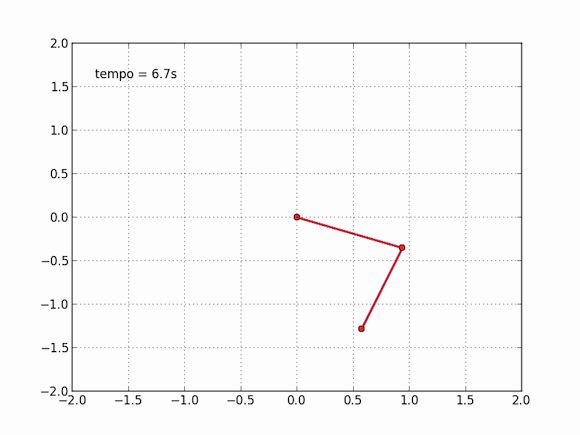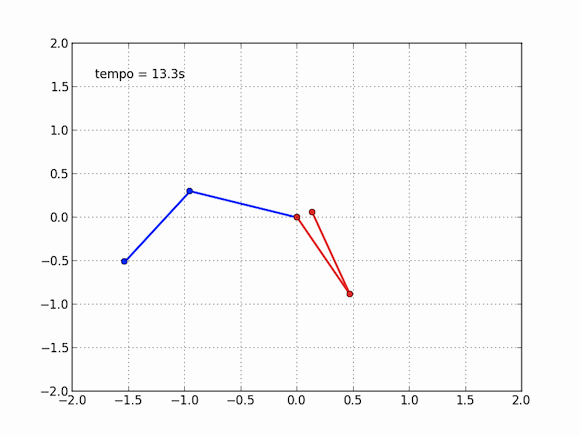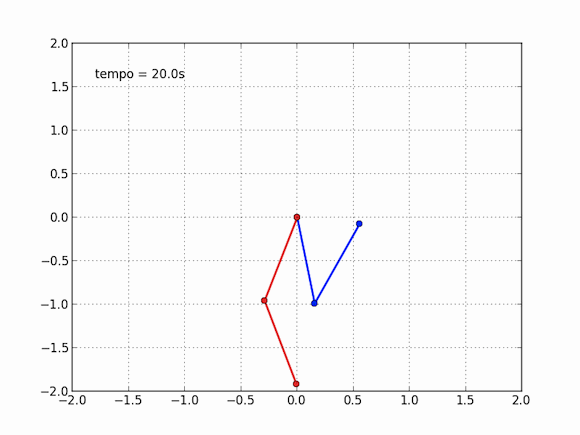

O efeito borboleta é uma possível interpretação dessa propriedade de sistemas caóticos. 10° e 9,9999° são muito próximos, mas em dez segundos os pêndulos passam a ser completamente diferentes, é impossível dizer que eles já estiveram juntos. Analogamente, as equações da mecânica dos fluidos são também muito difíceis de resolver, e apresentam comportamento caótico. Nesse pequeno gif, você percebe a influência de uma variação de 0,0001° na posição inicial de uma das bolinhas. Para a meteorologia, podemos perguntar: pode o bater de asas de uma borboleta no Brasil causar um tornado no Texas?